欧拉变换公式三角函数(利用欧拉定理对三角函数和差公式降维打击)
100次浏览
发布时间:2024-09-12 09:21:00
复数欧拉定理
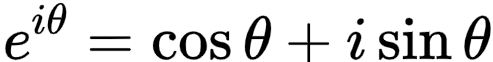
该公式搭建了复数与指数函数之间的桥梁,而复数又可以用三角函数表示,所以该公式也搭建起了三角函数与指数函数的桥梁。
如此,利用该公式,很多三角函数的问题可以用指数函数来解决。
该公式的证明有很多种方法,如麦克劳林展开式(Maclaurin's Series)。

降维打击三角函数和差公式
根据欧拉定理
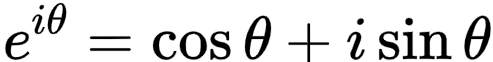
得
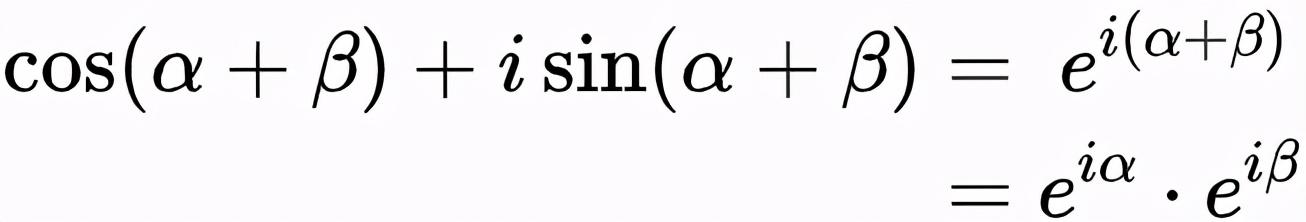
式(1)
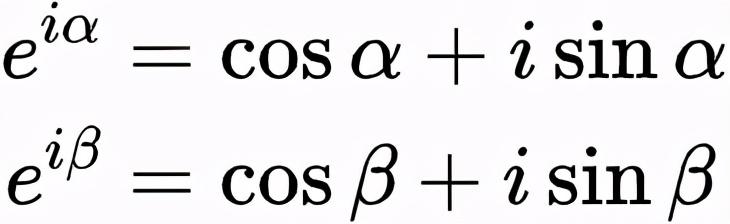
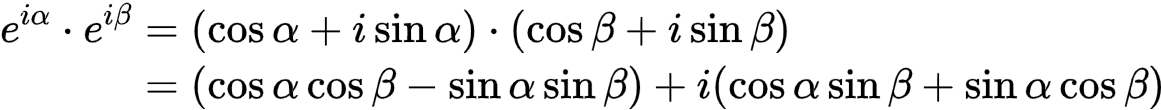
式(2)
对比(1)式和(2)式,即得到和的三角公式:
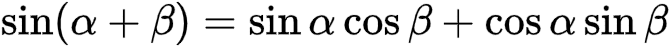
式(3)
式(3)
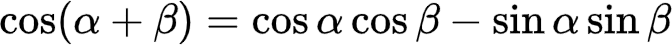
式(4)
对上述β取反,得到差的三角公式:
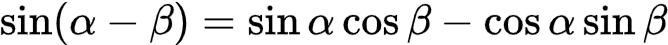
式(5)
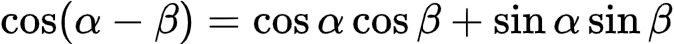
式(6)
积化和差公式
(6)-(4)得积化和差公式:
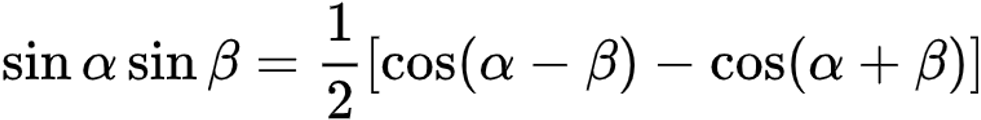
式(7)
(3)+(5)得积化和差公式:
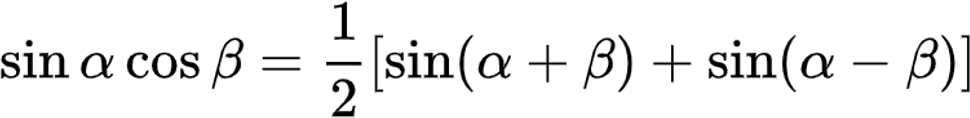
式(8)
(3)-(5)得积化和差公式:
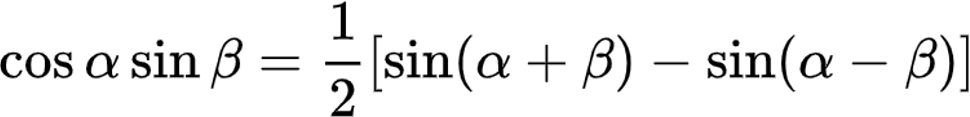
式(9)
(4)+(6)得积化和差公式:
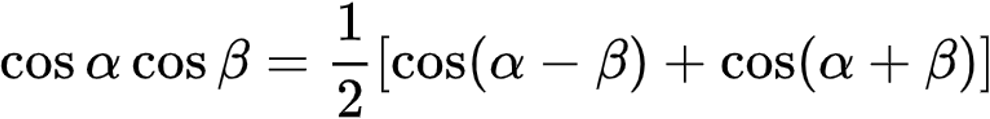
式(10)
和差化积公式
利用式(8),求得
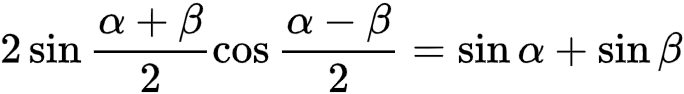
也即
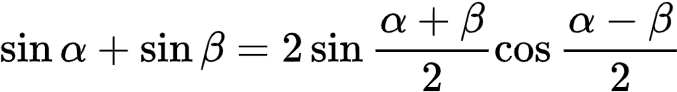
同样的方法,可以求得
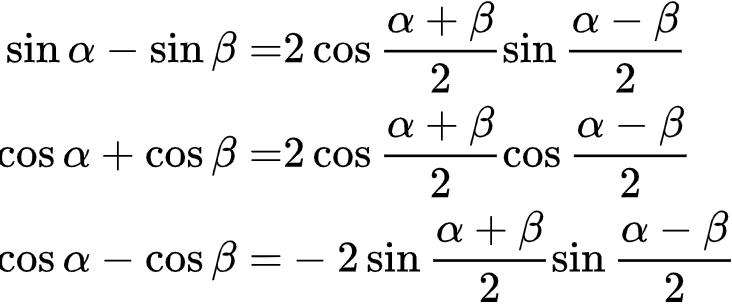
- 三角函数降幂公式与半角公式
式(7)中,令β=α,则得到
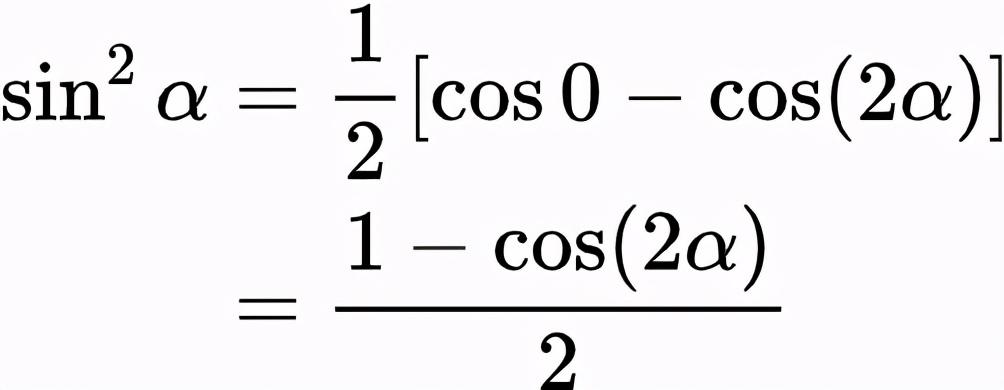
对上式中的α取半,得到降幂公式
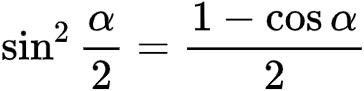
进而得到半角公式
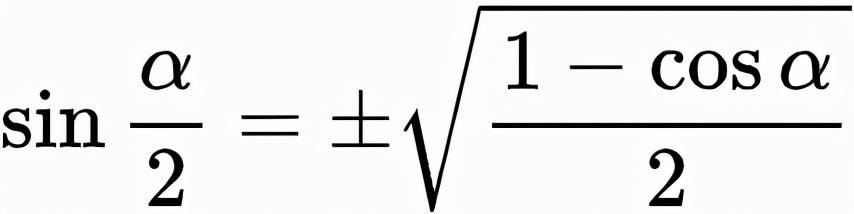
同样,式(10)中,令β=α,则得到
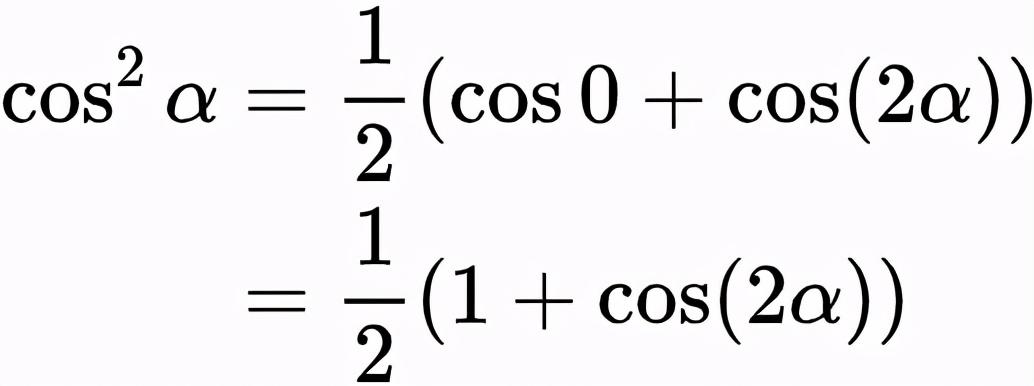
对上式中的α取半,得
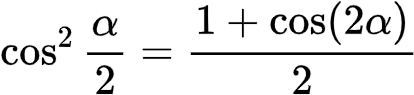
进而得到半角公式:
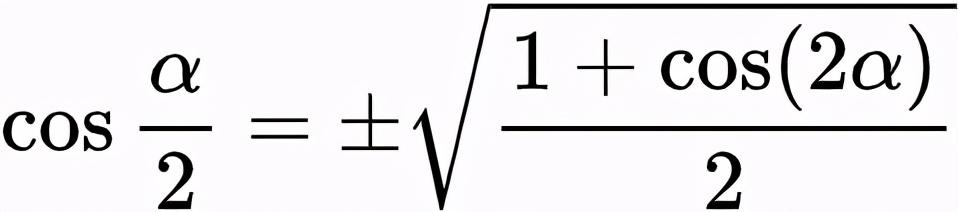
- 心得
不同的三角函数之间存在关联,有时候可以相互转化,由一个公式可以推导出另一个公式。学习者达到融会贯通的境界时,能从中获得一种乐趣。
相关文章
-
品友集成灶全国各市售后热线号码实时反馈-今-日-更-新 品友集成灶作为家庭中重要的安全设备之一,其专业服务质量直接关系到用户的使用体验和资产安全。品友集成灶24小时售后服务热线:400-883-2... 2025-04-22 00:03:51
-
格林姆斯热水器维修服务中心|全天24小时服务热线实时反馈全+境+到+达 格林姆斯热水器全国售后客服电话为400-883-2086,该电话开通时间为每周一至周五08:00-24:00,周六、周日08:00-23:0... 2025-04-21 23:58:19
-
得耐特指纹锁/全国各市服务热线号码实时反馈-今-日-汇-总 得耐特指纹锁售后服务维修电话:400-883-2086得耐特指纹锁24小时维修客服热线:400-883-2086得耐特指纹锁24小时服务电话... 2025-04-21 23:57:59
-
HOPO指纹锁售后24小时联系方式维修查询实时反馈-今-日-汇-总 我们了解,每一个家庭的HOPO指纹锁都是守护健康的重要伙伴,因此,我们的使命就是确保这些伙伴始终处于最佳状态。HOPO指纹锁售后客服电话:4... 2025-04-21 23:56:54
-
风田集成灶客服号码售后号码大全及维修网点查询实时反馈-今-日-更-新 风田集成灶24小时售后维修电话:400-883-2086上门时间:20分钟内响应上门收费标准:上门检测为准,报价后可选择是否维修。维修说明:... 2025-04-21 23:54:46
-
林内热水器各24小时售后全国客服受理中心实时反馈-今-日-资-讯 林内热水器团队由一群经验丰富、技术精湛的专业技师组成,他们不仅精通各类保险柜的内部结构与解锁技术,更对市面上主流及部分特殊型号产品的维护维修... 2025-04-21 23:52:57
-
火车头指纹锁售后维修号码-人工售后号码实时反馈-今-日-汇-总 火车头指纹锁的维修电话可能因地区和具体服务内容而有所不同,但通常,用户可以通过拨打火车头指纹锁的客服热线来获取维修服务。以下是一些可供参考的... 2025-04-21 23:52:10
-
皇浩裕指纹锁全国统一售后24小时受理客服中心实时反馈-今-日-资-讯 皇浩裕指纹锁作为国内知名的安全门品牌,一直以卓越的品质和周到的服务赢得了广大消费者的信赖。为了更好地服务每一位用户,皇浩裕指纹锁特别设立了2... 2025-04-21 23:51:57
-
富士通空调24小时售后服务热线实时反馈-今-日-资-讯 富士通空调售后服务维修电话:400-883-2086富士通空调24小时维修客服热线:400-883-2086富士通空调24小时服务电话《今日... 2025-04-21 23:50:02
-
卢纳森智能锁全国各市售后服务点热线号码实时反馈-今-日-资-讯 亲爱的用户朋友们,相信大家在使用卢纳森智能锁时,一定遇到过一些小麻烦,比如说,有时候会遇到无法解锁的情况。今天我就来和大家聊聊这个话题,从三... 2025-04-21 23:47:15







